前言
上篇博客中提到了空间索引的用途和多种数据库对空间索引的支持情况,那么在应用层以下,好学的小伙伴应该会考虑空间索引的实现原理了。
目前空间索引的实现有 R树和其变种GIST树、四叉树、网格索引等。 网格索引不再多提,使用普通的hash表存储地点和风格之间的映射来实现。今天要介绍的GeoHash算法实现的空间索引,虽然是以B树实现,但我认为它也借用网格索引的一部分思想。
GeoHash
原理
GeoHash 算法的原理说起来是很简单的,如下图:
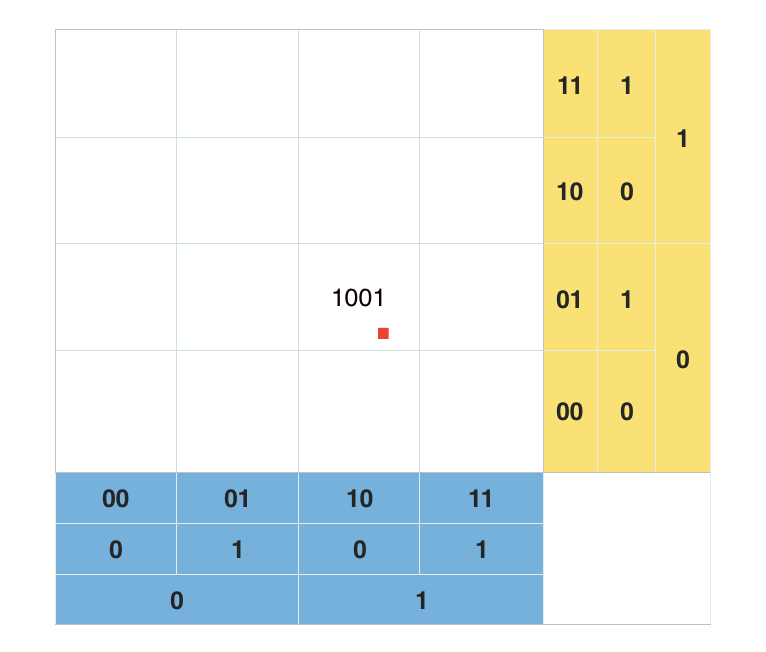
- 从横向上将整个方形纸分为左右两份,左侧部分为标记为
0, 右侧部分标记为1; - 再将红点所在的部分划分为左右两块,再对红点位置做同样的标识,最后得出红点在横向上的标识为
10; - 在纵向上对方形纸做同样的划分,左侧标识为
0,右侧标识为1,得出红点位置在纵向上的标识为01; - 将横向标识和纵向标识合并,规则为
纵向在奇数位,横向在偶数位(也可纵横相反,但要在整个系统内保持一致),得出红点在方形纸上的标识为1001;
只标记一个方格显得看不出什么规律,如果我们把这些都空格都标识后会发现 被划分在角落里的四个方格会有同样的前缀,如下图所示。

同样的前缀意味着可以使用 B树 索引查找有相同前缀的点作为附近的点,GeoHash 算法便是这些同样的前缀上面做文章。
墨卡托投影
墨卡托投影,是正轴等角圆柱投影。由荷兰地图学家墨卡托(G.Mercator)于1569年创立。假想一个与地轴方向一致的圆柱切或割于地球,按等角条件,将经纬网投影到圆柱面上,将圆柱面展为平面后,即得本投影。墨卡托投影在切圆柱投影与割圆柱投影中,最早也是最常用的是切圆柱投影。
墨卡托投影简单地说,就是可以 把整个地球平面作为一个正方形来处理,当然地球平面不是严格的正方形,此投影在两极附近的点会有误差,本文专注于原理,纠偏就不多提了(我也不懂,逃)。
实现
按照墨卡托投影的平面,我们可以按照上面划分方格纸的方式来将整个地球表面划分为各个小方格。
如(116.276349, 40.040875)这个点的经度划分:
- 经度在 [-180,0) 范围内的标识为
0,经度范围在 [0, 180) 度的标识为1; - 继续划分,经度范围在 [0,90) 的标识为
0,经度范围在 [90,180) 的标识为1; - 这样,我们划分 20 次,方格的精度(见文末对照表)已达到 2m,得到经度的标识二进制串为
11010010101011110111; - 对纬度同样划分,得到纬度的标识二进制串为
10111000111100100111; - 我们对它组合,得到40位的二进制串
11011 01110 00010 01110 11100 10111 01001 11111; - 我们将这个二进制串使用
base32编码(原理同base64,可以见我的另一篇文章:,位编码映射表见下),得到 GeoHash 编码为3OCO4XJ7;
那么GeoHash编码前缀为 3OCO4XJ7的地理点就是离 (116.276349, 40.040875)两米内的点。如果我们把地理位置点和其GeoHash编码存入数据库的话,我们要查找 附近两米点的点,只需要限定条件 geo_code like '3OCO4XJ7%'就行了;
边界点问题
可是最简版的 GeoHash 还有一个弱点,如下图:
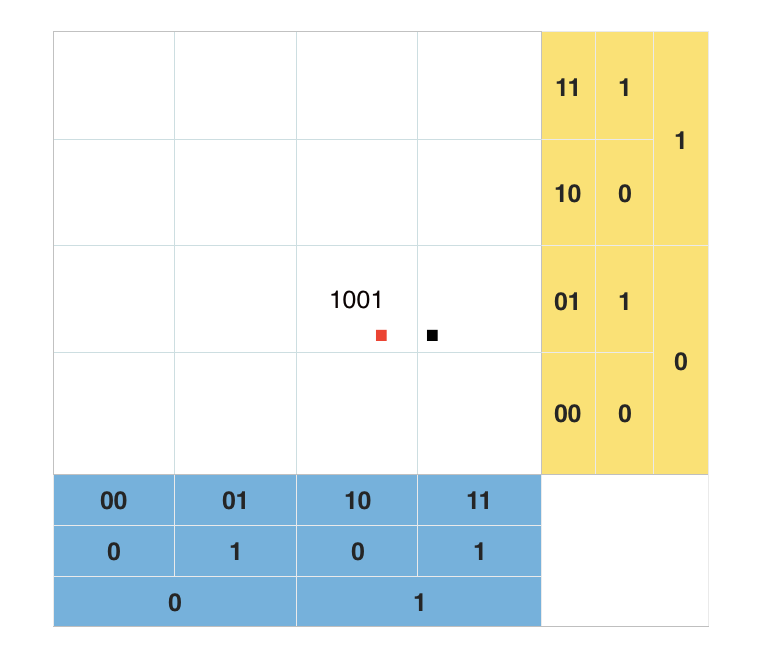
如果每个方格的精度为 2km,那么我们直接按照前缀查询红点附近 2km 的点是查找不到离它很近的黑点的。
要解决这个问题,我们就需要所其周边八个方格也考虑上,将自身方格和周边八个方格内的点都遍历一次,再返回符合要求的点。那么如何知道周边方格的前缀呢?
仔细观察相邻方格,我们会发现两个小方格会在 经度或纬度的二进制码上相差1;我们通过 GeoHash 码反向解析出二进制码后,将其经度或纬度(或两者)的二进制码加一,再次组合为 GeoHash 码。
Redis的GEO函数
问题
我们常见的需求是查找 n米 范围内的点,那么 n米 与 GeoHash 码位数之间的映射如何实现呢?由于 GeoHash 码是由5位二进制码组成,每少一位,精度就会损失 2e(5/2)。
方法当然有的,我们将二进制GeoHash码直接索引就可以,但很长的索引长度会导致 B树 索引查询效率会迅速下降。
方案
于是我们接着寻找解决方案,既然使用 base32 转换为 32进制码 会不好控制精度,保持二进制又导致索引长度过长,那么进制位数和索引长度有没有一个平衡呢?
另外 Redis 的 sorted set 支持 64位 的 double 类型的 score,我们把二进制的 GeoHash 码转为十进制放入 Redis 的 sorted set 中,不是可以实现 log(n)的查询效率了么。
说实话第一次看到 Redis 的 GEO 系列函数的时候我的内心是崩溃的,原来自己感觉极其良好的设计早已被人实现了(虽然这种情况经常出现)。。。
当然不能就这么算了,于是我使用PHP造了一遍轮子。。。
主要步骤如下:
代码实现
实现中我将 GeoHash 的最大精度设置为26位,此时它的距离精度为 0.3m。当然我们也可以充分利用 Redis 的 sorted set 的 score,设置精度为 32 位,刚好使用它的 double 类型。
放上GitHub源码地址:
数据入库:
将经纬度通过 GeoHash 算法获取到二进制 GeoHash 码,并将其转成十进制作为这个点的 score 存入 Redis 的 sorted set;
// GeoHash核心方法 传入float类型的度数和其对应的范围,经度和纬度公用方法public function getBits($loc, $range, $level = self::LEVEL_MAX) { $bits = ''; for ($i = 0; $i < $level; $i++) { $mid = ($range['min'] + $range['max']) / 2; if ($loc < $mid) { $bits .= '0'; $range = ['min' => $range['min'], 'max' => $mid]; } else { $bits .= '1'; $range = ['min' => $mid, 'max' => $range['max']]; } } return $bits;} 另外 php 的 bindec($bin_str) 方法能快速把二进制字符串转为十进制数字。
根据查询范围半径获取精度
上文说过,精度是由地图的划分次数决定的,划分次数多了,范围就小了,查询的出的数据就不全;划分次数少了,范围就会大了,我们对数据过滤时就会有过多的损耗。
private function getLevel($range_meter){ $level = 0; $global = self::MERCATOR_LENGTH; while ($global > $range_meter) { $global /= 2; $level++; } return $level;} 上面代码的思想来自redis geo函数源码,真的很巧妙。
在墨卡托投影下,地球的表面可以作为一个正方形来看,它的边是地球周长中最长的一个。而学过初中地理的我们知道:“地球是一个两极稍扁,赤道略鼓的球体”,那么它最长的一个周长就是赤道周长了,于是我们得知墨卡托投影的长边为 2*PI*R=40075452.74M;
于是我们拿正方形的一个边来不停地进行二次划分,直到划分后的结果刚好比范围半径长,那么它构成的一个方块,便是我们需要的方格。
数据查询
数据查询时,我们需要获取中间方块的最小 score 值和其范围,最小 score 值很简单,直接将二进制位不足52位的在后面补0。
此外,为了避免边界点问题,我们还需要把周围八个方格的 score 值范围也获取到。
我们在划分地图时,每多划分一次,会添加经度和纬度两个二进制位,在精度最高时,那么每一个方格的最大值和最小值之间差1。由此,我们通过下面的方法获取到一个方格的最大和最小 score 值之差。
private function getLevelRange($level) { $range = pow(2, 2 * (self::LEVEL_MAX - $level)); return $range;} 再由上面提过的边界点问题的解决方案,获取到周边八个方格的最小 score 值。
使用 Redis 的ZRANGEBYSCORE key hashInt hashInt+range命令将这九个方格内的点全部取到,再遍历九个方格,将距离不符合的数据过滤掉。
小结
花费了十多个小时,总算将 GeoHash 完全整体了一遍,完全理解 GeoHash 并没有想像中的那么简单。除了 GeoHash,四叉树和R树据说查询效率会更高,有时间再研究一下。
如果您觉得本文对您有帮助,可以点击下面的 推荐 支持一下我。博客一直在更新,欢迎 关注 。
参考:
GeoHash位数精度对照表(wiki百科):
| GeoHash length | lat bits | lng bits | lat error | lng error | km error |
|---|---|---|---|---|---|
| 1 | 2 | 3 | ±23 | ±23 | ±2500 |
| 2 | 5 | 5 | ±2.8 | ±5.6 | ±630 |
| 3 | 7 | 8 | ±0.70 | ±0.70 | ±78 |
| 4 | 10 | 10 | ±0.087 | ±0.18 | ±20 |
| 5 | 12 | 13 | ±0.022 | ±0.022 | ±2.4 |
| 6 | 15 | 15 | ±0.0027 | ±0.0055 | ±0.61 |
| 7 | 17 | 18 | ±0.00068 | ±0.00068 | ±0.076 |
| 8 | 20 | 20 | ±0.000085 | ±0.00017 | ±0.019 |
base32 编码映射表:
| Value | Symbol | Value | Symbol | Value | Symbol | Value | Symbol |
|---|---|---|---|---|---|---|---|
| 0 | A | 9 | J | 18 | S | 27 | 3 |
| 1 | B | 10 | K | 19 | T | 28 | 4 |
| 2 | C | 11 | L | 20 | U | 29 | 5 |
| 3 | D | 12 | M | 21 | V | 30 | 6 |
| 4 | E | 13 | N | 22 | W | 31 | 7 |
| 5 | F | 14 | O | 23 | X | ||
| 6 | G | 15 | P | 24 | Y | ||
| 7 | H | 16 | Q | 25 | Z | ||
| 8 | I | 17 | R | 26 | 2 |